1 案例背景
根据裂纹的破坏情况,裂纹被分为张开型(Ⅰ型)、滑开型(Ⅱ型)和撕开型(Ⅲ型),其中Ⅰ型裂纹是最基本的类型(图 1-1),也是工程中常见的破坏类型,研究裂纹尖端附近应力场分布对于预防工程中发生的断裂破坏具有重要意义。
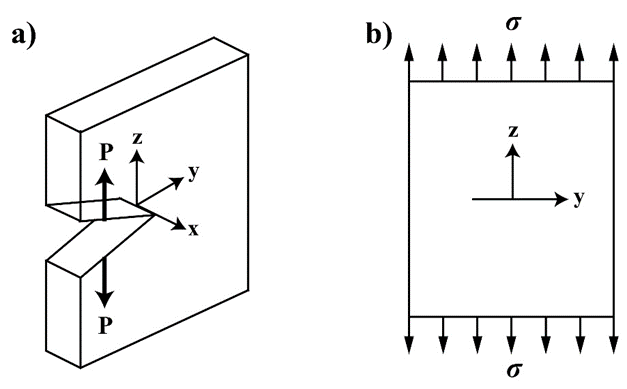
图1-1 (a) Ⅰ型裂纹示意图 (b) Ⅰ型裂纹受力图
本报告对Ⅰ型裂纹尖端应力场分布进行了数值模拟计算,同时与利用Westergaard应力函数得到的解析解进行了对比,从不同角度比较了FssiCAS、Abaqus、FLAC3D对于Ⅰ型裂纹尖端应力场的计算结果可靠度,评估了各类模拟方法的可行性,具体内容包括:
(1) 对比FssiCAS与Abaqus专有裂纹计算模块之间的计算差别,同时与解析解进行对比验证。
(2) 考虑到裂纹在实际过程中并不是椭圆形,进而在FssiCAS中尝试设置相同位置的非接触节点对裂纹进行模拟,对计算结果进行分析。
(3) 对比FssiCAS与FLAC3D计算结果差异,两者分别代表有限单元法和有限差分法,计算思路存在不同。
依据该Ⅰ型裂纹模型,建立沿y轴的对称模型进行计算。
2 FssiCAS模拟及与Abaqus专有裂纹计算模块对比
本节对FssiCAS模拟过程进行说明,同时将结果与解析解和Abaqus专有裂纹计算模块结果进行对比,具体过程如下。
2.1 模型建立
FssiCAS支持多种类型的网格导入,本模拟选用Abaqus建立网格及背景线文件,可在Abaqus中完成网格建立以及材料属性设置过程,在完成装配后导出最终网格。
2.1.1 Abaqus划分网格
(1) 绘制草图,将裂纹视为一椭圆形预制槽
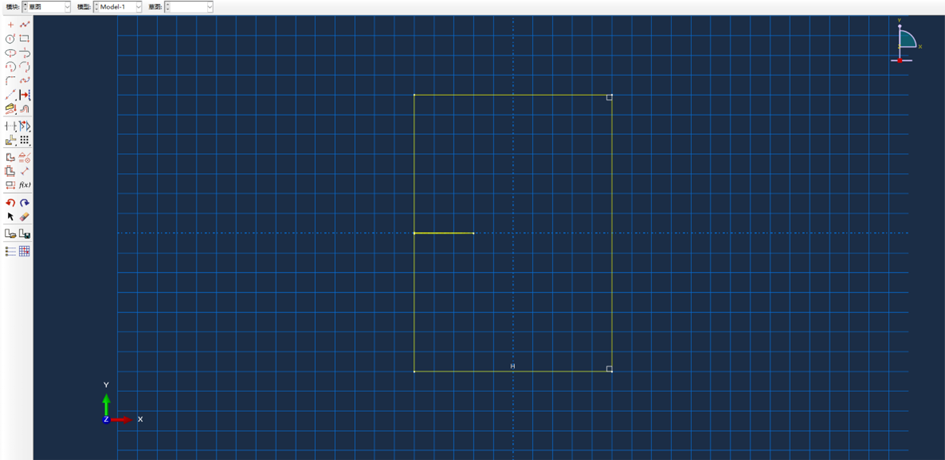
图 2-1 数值模型边界草图
(2) 创建部件,定义实体,部件选择二维平面,基本特征选择壳。

图 2-2 定义部件过程示意图
(3) 定义材料,及将材料指定到部件单元上,注意此处命名尽量一致,否则可能出现导入错误。
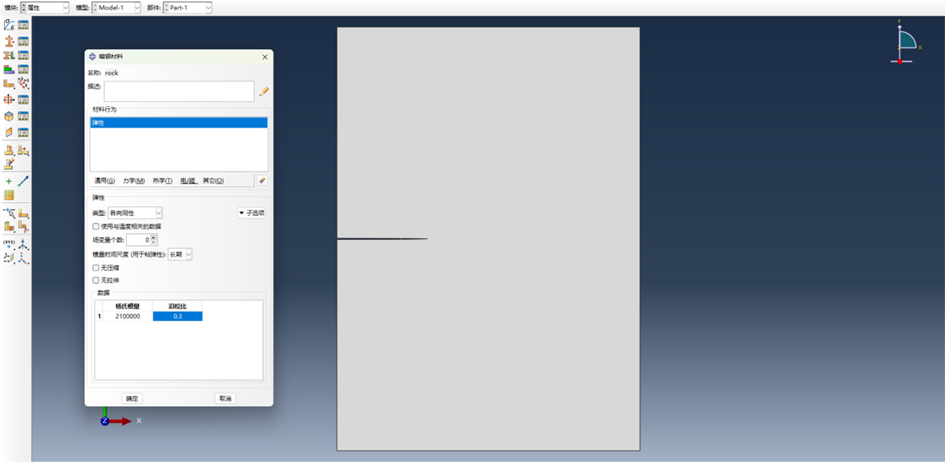
图 2-3 定义材料属性

图 2-4 将材料赋予指定截面
本次模拟仅涉及一种材料。
(4) 网格划分,Abaqus中可以设置网格的类型以及网格的密度等参数,本次模拟选用六节点三角形单元,提高计算的准确性。考虑到后续需要提取指定线条上应力分布曲线,在划分网格过程中需要确保指定线条上存在节点,因此在划分网格阶段重新对截面进行二次划分。同时对靠近裂纹尖端处的网格进行加密处理
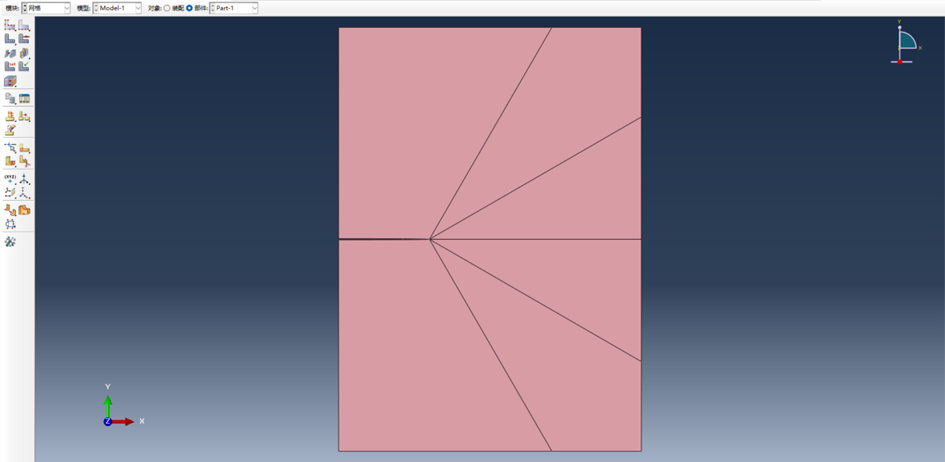
图 2-5 截面二次划分
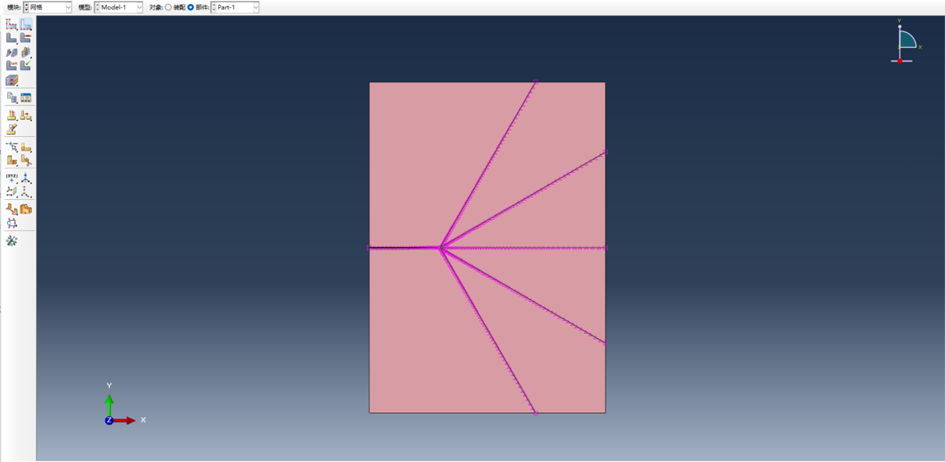
图 2-6 网格加密

图 2-7 网格划分
(5) 建立装配,导出网格及背景线

图 2-8 建立装配
建立作业,在作业管理器中导出.inp文件,同时导出背景线文件。
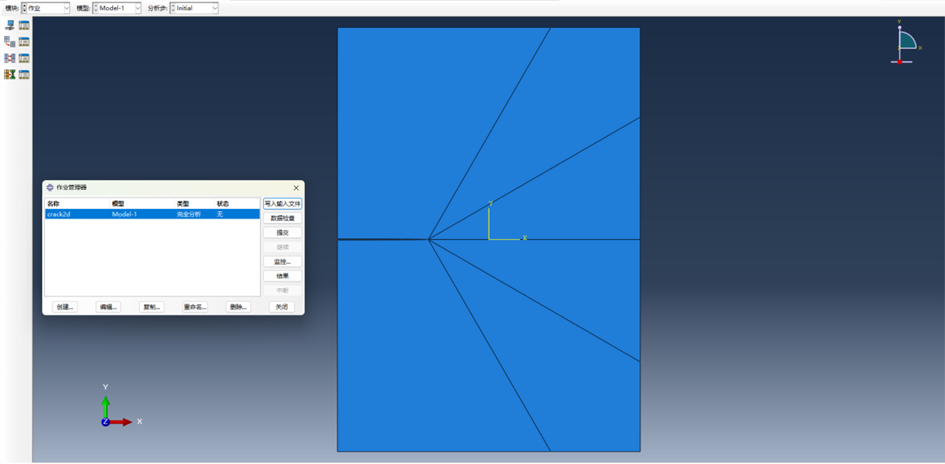
图 2-9 导出网格文件
到此完成网格导出。
2.1.2 FssiCAS导入模型及定义
(1) FssiCAS模型导入
选择从Abaqus中导入网格文件,不涉及流体单元,直接导入即可。
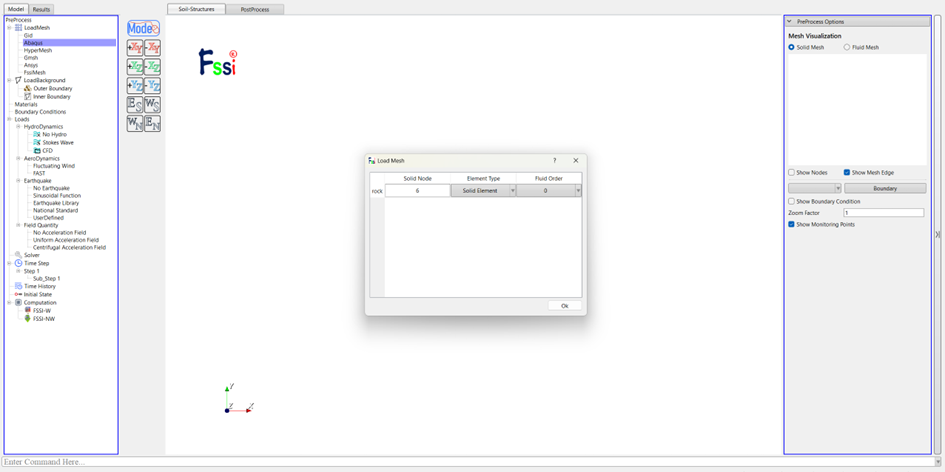
图 2-10 导入网格文件
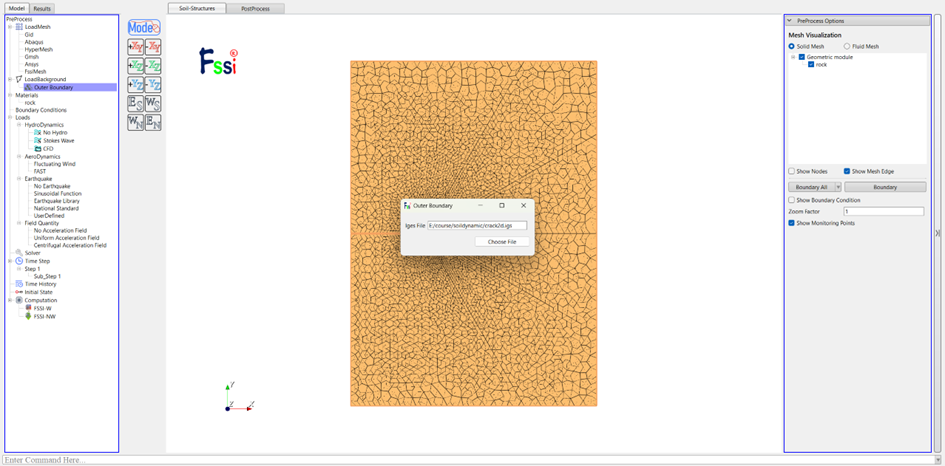
图2-11 模型背景线导入
(2) 材料属性定义
本次模拟选择材料参数为弹性模量2.1e6Mpa,泊松比设置为0.3。考虑到解析解基本假设为线弹性材料,所以选择elastic本构。
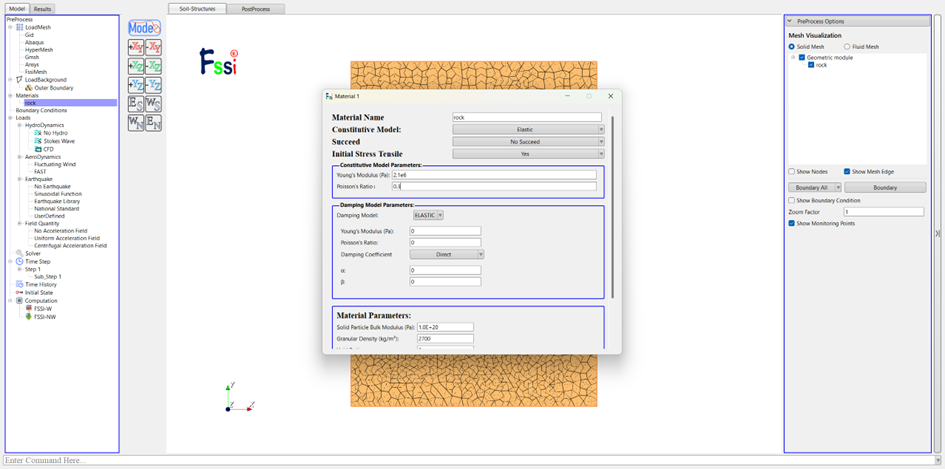
图 2-12 定义模型材料
(3) 边界条件施加
对于Ⅰ型裂纹而言,其破坏模式为张开型,所以对模型上下边界同时施加大小为2000Pa的均布拉力,为防止模型的刚体位移,在远离裂纹端的中间节点施加固定约束。
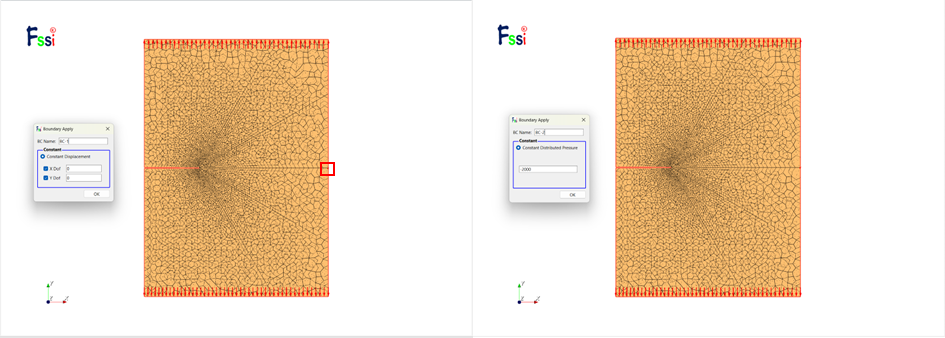
图 2-13 定义模型边界条件
(4) 定义计算参数,设置无水,无体积力,计算模式选择二维平面应力求解,同时设置不更新刚度矩阵与节点坐标,具体设置如图2-14所示。
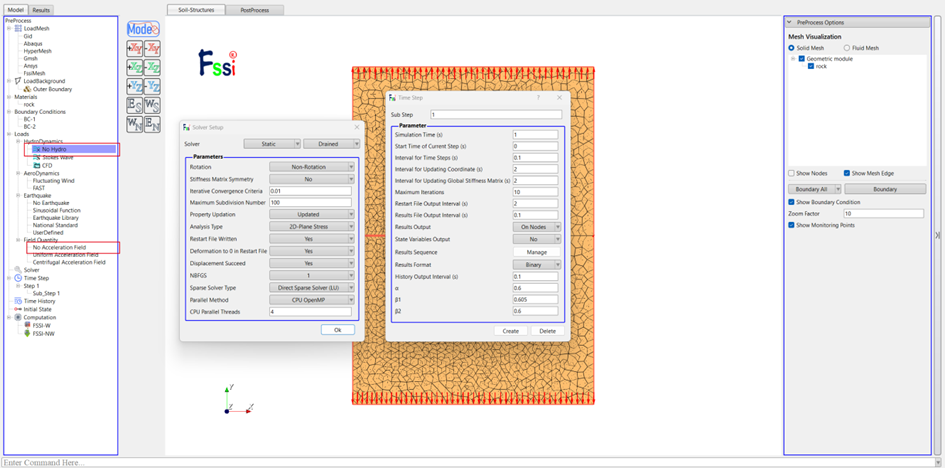
图 2-14 定义计算参数
至此已经完成全部模型计算前的工作,在状态初始化后即可开始计算。
2.2 模型计算结果及对比
2.2.1 Abaqus专有裂纹计算模块
Abaqus专有裂纹计算模块包含现有常用裂纹计算方法,如J积分,XFEM等,可以定义裂纹初始端与扩展端,进而计算裂纹的扩展路径等。对模型进行相应设置,模型尺寸、参数以及边界条件等设置与FssiCAS计算模型相同。计算弹性状态下的裂纹尖端附近的应力场分布情况。
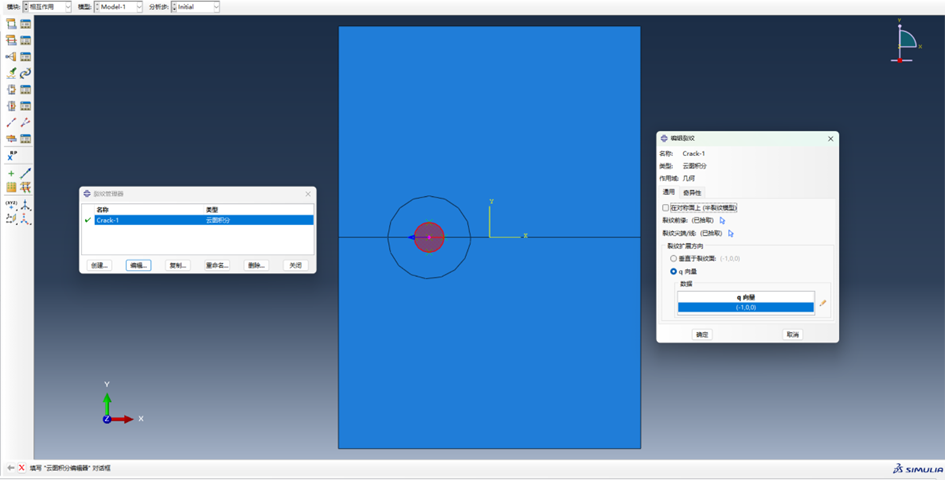
图 2-15 Abaqus裂纹计算模块
此情况下,对裂纹附近的网格划分要求较低,因为尖端处存在节点,无需过度加密网格即可。
图 2-16 Abaqus裂纹计算网格划分
2.2.2 FssiCAS与Abaqus结果云图对比
提取FssiCAS与Abaqus的计算结果云图进行对比,两种计算方法对于Ux的云图有一定差异,FssiCAS的计算结果更符合对称性,但是相较于模型尺寸而言,模型的位移均较小,差别可忽略不考虑。对于Uy的计算,FssiCAS的计算结果更符合对称性,Abaqus的误差相对较大,考虑可能是因为网格划分不均匀导致。
对于应力的计算结果,两者均可较好的模拟出裂纹尖端的应力集中现象,对于σxx和σyy的计算结果相近,由于计算方法不同,尖端的应力极值存在一定差异。
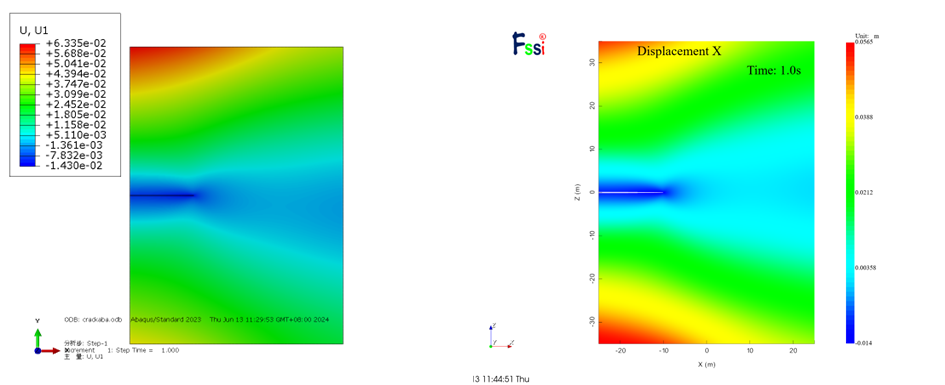
图 2-17 Ux计算结果云图对比
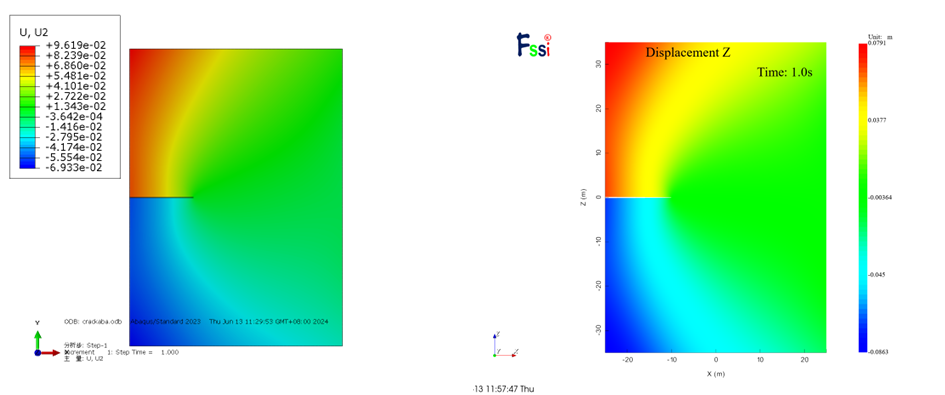
图 2-18 Uy计算结果云图对比
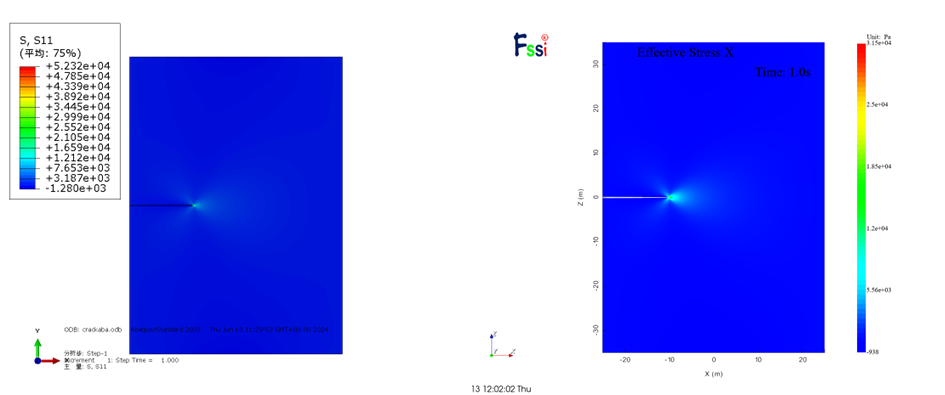
图 2-19 σxx计算结果云图对比
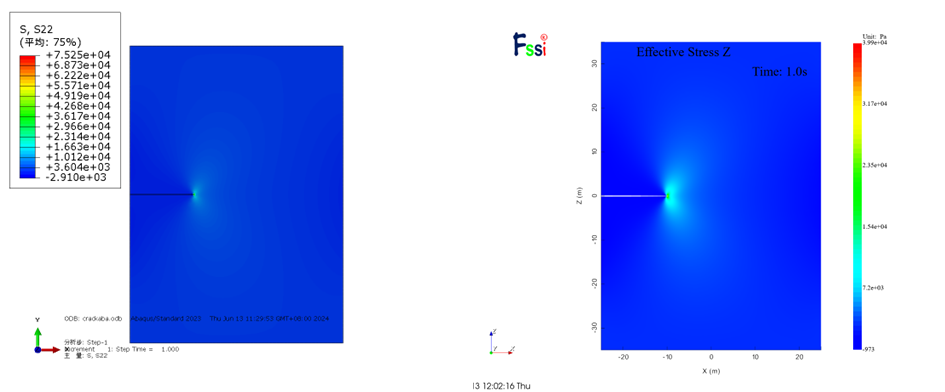
图 2-20 σyy计算结果云图对比
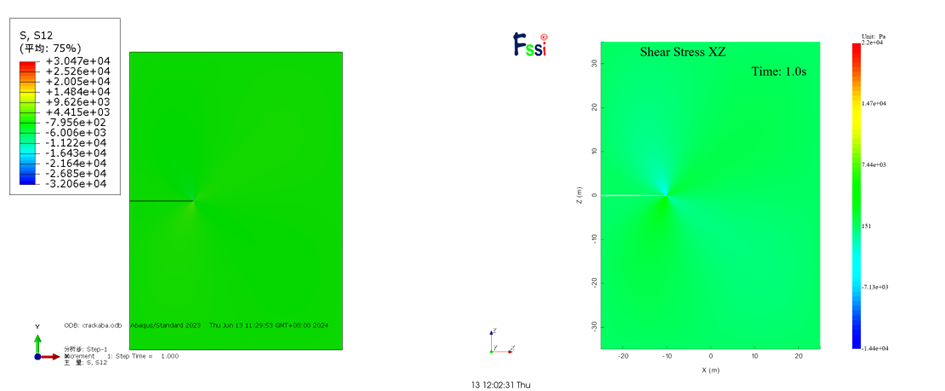
图 2-21 σxy计算结果云图对比
2.2.3 解析解结果对比
为进一步比较两者的计算准确性,单独提取特定角度线上的应力分布进行与解析解的对比验证,分别选择θ = 0°,θ = 30°以及θ = 60°线上的应力解进行对比。Abaqus中可以单独提取某一线段上的节点数据,FssiCAS对于倾斜直线上的节点应力提取相对麻烦,尤其在节点较多的情况下,故在本文在提取过程中使用python编写提取脚本,代码见附录一。首先导出输出文件后导入excel中,另存为csv文件进行应力提取。
最终提取结果如下,其中FssiCAS与Abaqus的计算结果基本一致,但由于Abaqus计算使用的是专有裂纹计算模块,在裂纹尖端,即奇异点处有单独处理模式,由此使得其在裂纹尖端的拟合程度较高。但是FssiCAS在没有特殊处理下,依然可以顺利完成对奇异点处的计算,虽然达到的极值相对较低,但仍说明了该软件的适用性。
两种计算方法对于σxx和σyy的计算结果在距离尖端,即奇异点处的准确性较高,而在远离奇异点处,由于模型的边界效应存在,导致靠近模型边缘的结果有一定程度的偏移,但处于可接受范围内。
对于σxy的计算结果则偏差较大,尤其是在应力尖端附近,由于网格划分以及计算误差导致尖端附近位移存在一定程度的不对称性,由此导致剪切应力在应力尖端附近误差较大,会出现明显波动,即便是Abaqus的专有裂纹计算模块也无法处理剪应力在奇异点处的问题,但在远离尖端处,两者的计算结果相对误差较小,尤其是在θ = 0°线上,两者在远端的解都接近解析解,即零值。
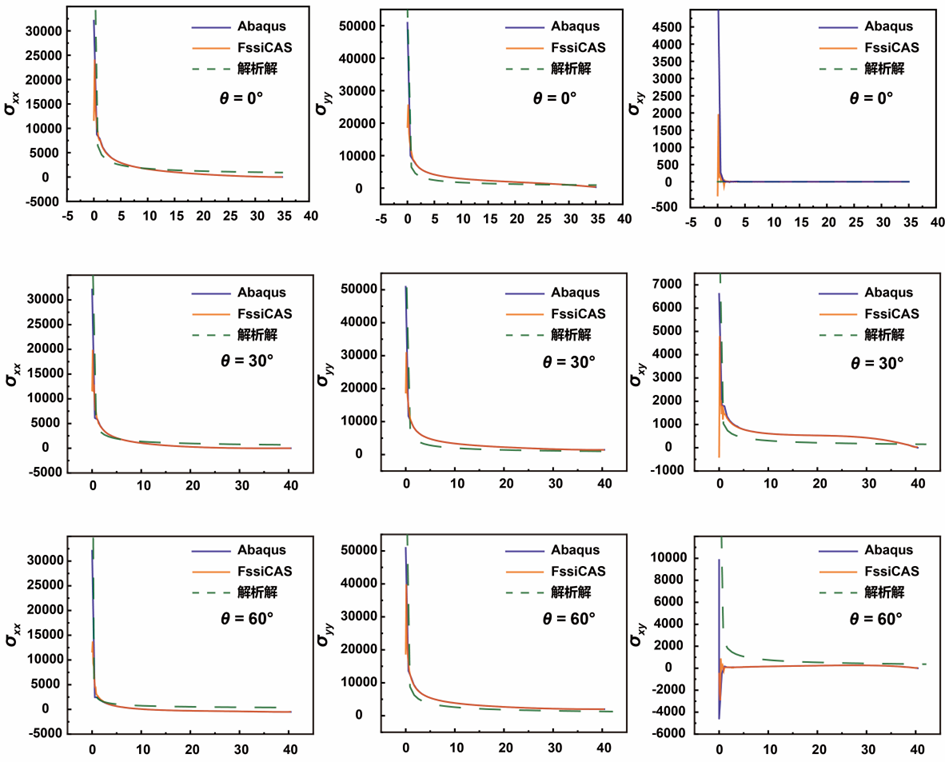
图 2-22 FssiCAS, Abaqus及解析解结果对比
在计算时长方面,FssiCAS具有较大优势,计算过程几乎不需要等待,而Abaqus的计算时长达到了十二秒,与模型内部组合刚度矩阵过程等因素有关。
2.3 本章小结
本章使用FssiCAS和Abaqus对裂纹尖端的应力场位移场进行了模拟计算,结果与解析解基本相同,在远离尖端处受边界效应影响有一定误差。虽然Abaqus使用了专有裂纹计算模块,在奇异点处处理较好,但与FssiCAS计算结果差异不大,说明了FssiCAS在裂纹弹性静力学分析中的适用性。
3 共坐标节点裂纹建模方法
在上一章中使用的裂纹建模方案是在裂纹位置开槽进行计算,虽然可以得到精度较高的结果,但网格数量较多,在更为复杂的裂纹建模中,这样的建模方法会导致模型单元数量成倍增加,影响计算效率。
本章试验了一种设置共坐标节点的裂纹建模方案,即在裂纹处设置坐标相同但序号不同的节点进行建模,可以避免需要在裂纹尖端加密网格的模式,降低了网格数量,提高了计算速度。与第二章中的建模方式进行对比,结果显示在应力分布上两种建模方式的计算结果基本相同,但在位移计算上存在较大差异,需要进一步改进。
3.1 共坐标节点裂纹建模方式
由于Abaqus划分网格并不支持直接划分共坐标节点,需要对其导出的网格信息文件进行二次处理后重新导入FssiCAS中进行计算,具体建模方式如下:
(1) 在Abaqus中建立不包含裂纹的长方形模型,但在裂缝所在位置画线,确保裂纹所在位置存在节点,基本过程与第二章中相同,最终得到.inp文件。
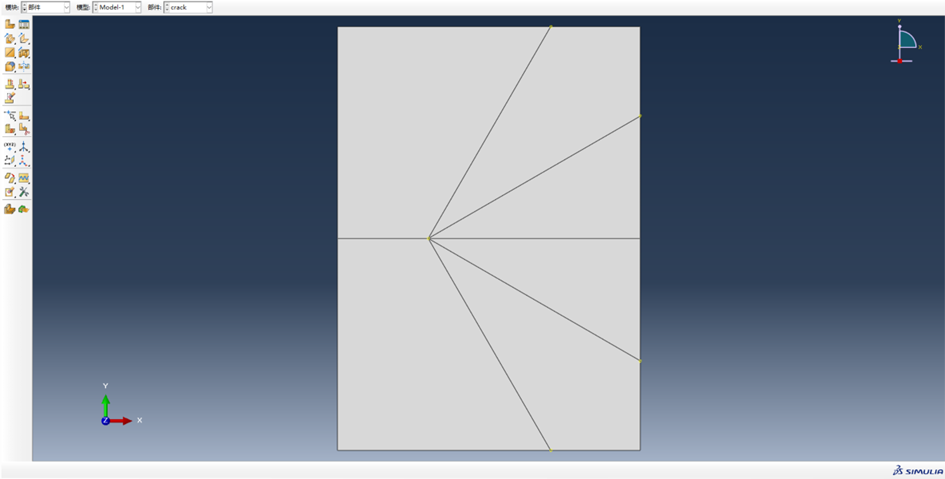
图 3-1 共节点裂纹网格初处理
(2) 将.inp文件以文本格式打开,其中包含了节点的坐标信息和每个单元的节点信息。(图3-2)
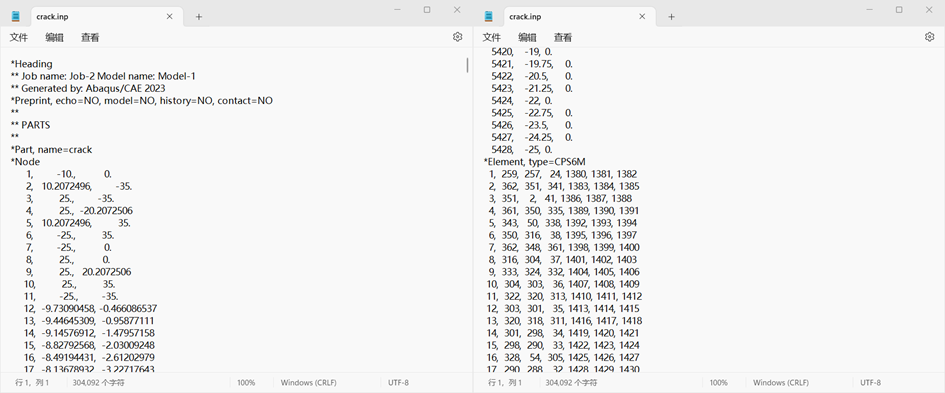
图 3-2 inp文件结构
(3) 提取位于裂纹位置上的节点,在excel中读取后复制在原有inp文件的节点之后,同时按照顺序定义新的节点编号。
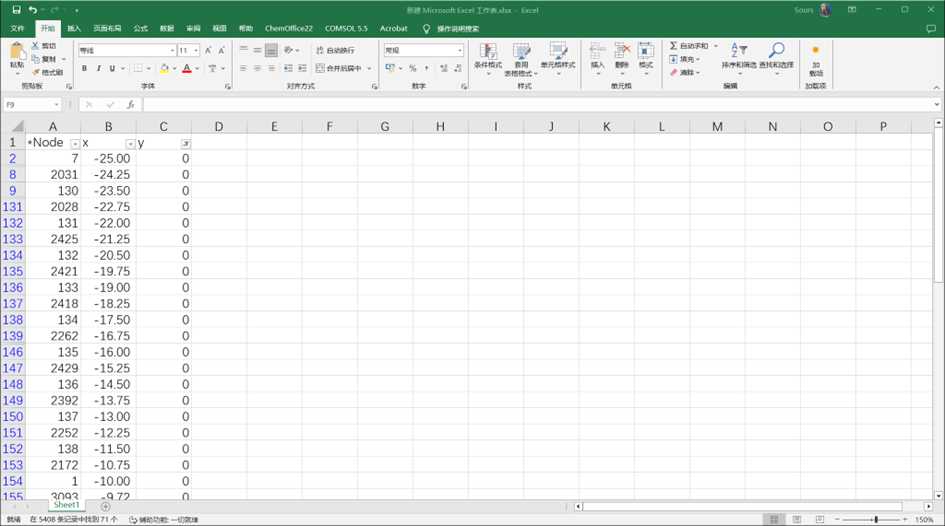
图 3-3 提取裂纹位置处的节点
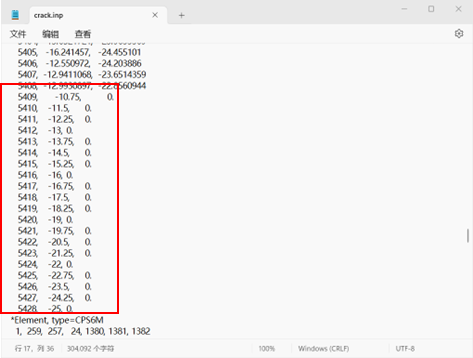
图 3-4 复制裂纹位置节点并设置新编号
(4) 调整单元中的节点编号,将裂缝上下单元中原本的共节点单元分离,在FssiCAS中识别裂缝下方单元编号,将其中的节点编号更新为新的节点编号。
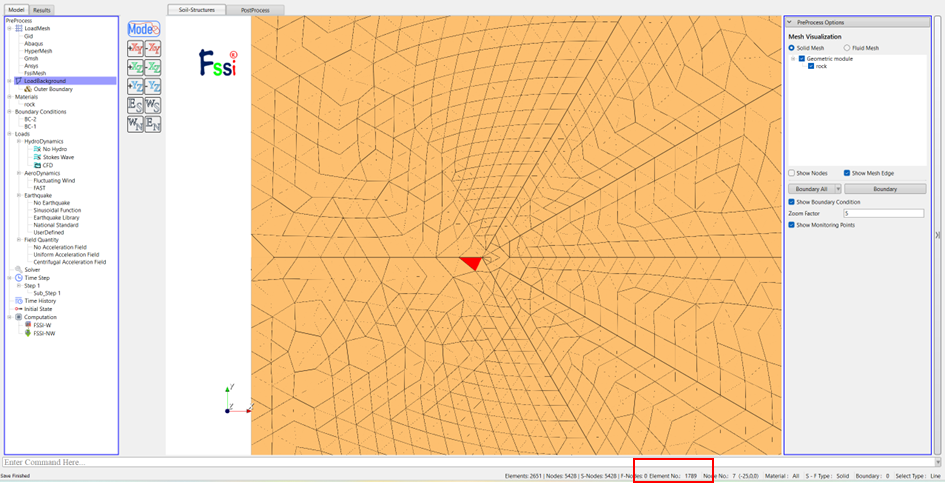
图 3-5 读取裂缝下方单元节点编号
图 3-6 更改对应单元中的节点编号
如原有1789号单元的六个节点为(993,1,138,4149,2252,4150),其中第138号节点和第2252号节点与裂纹上方单元共用,计算中无法张开,此处通过将节点更新为与这两个节点坐标一致但重新添加的新节点即(993,1,5410,4149,5409,4150),通过这样的方式将单元分离,完成裂纹建模。
(5) 将修改后的.inp文件重新导入,未出现错误信息,说明FssiCAS支持对于共坐标节点的处理。
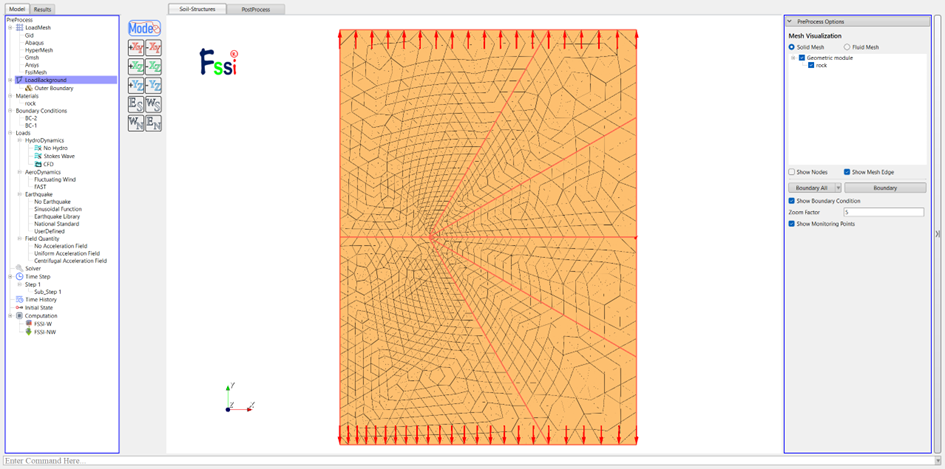
图 3-7 导入新inp文件
此时已经没有预制椭圆裂缝,但裂纹处的节点已经被分离,可以在拉力作用下张开。
3.2 两类建模方式计算结果对比
提取两种方法下的计算云图对比如下,左侧为原始建模方法,右侧为新建模方案
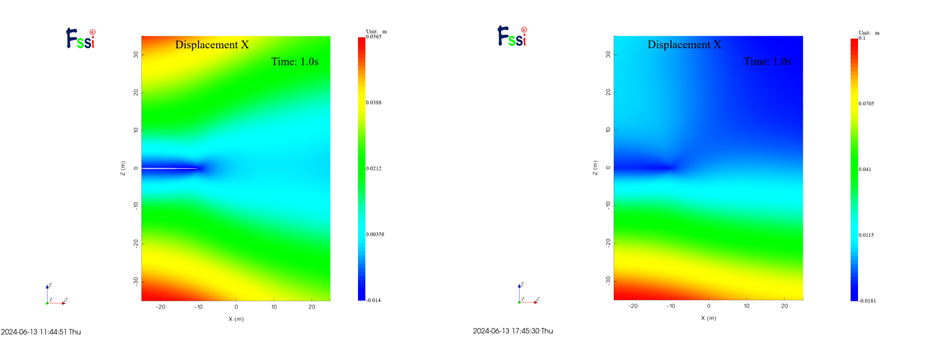
图 3-8 Ux计算结果云图对比
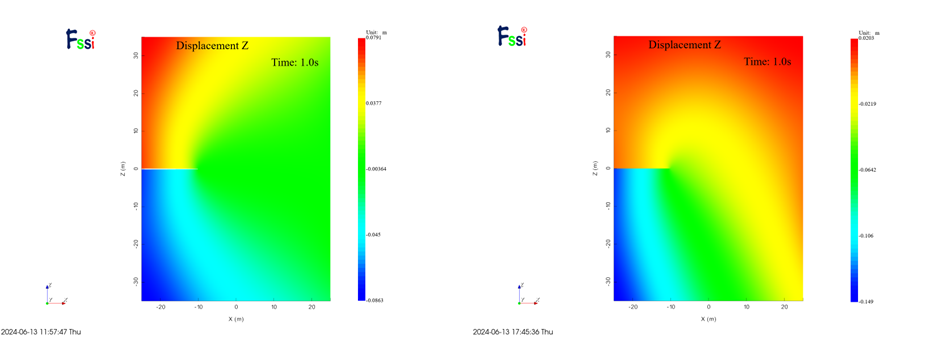
图 3-9 Uy计算结果云图对比
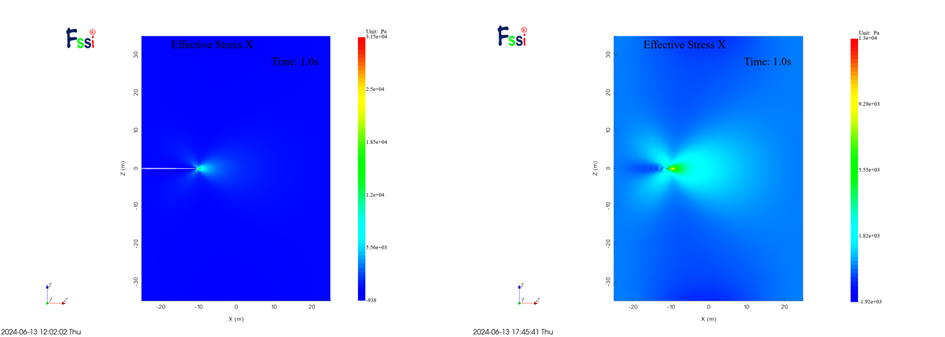
图 3-10 σxx计算结果云图对比
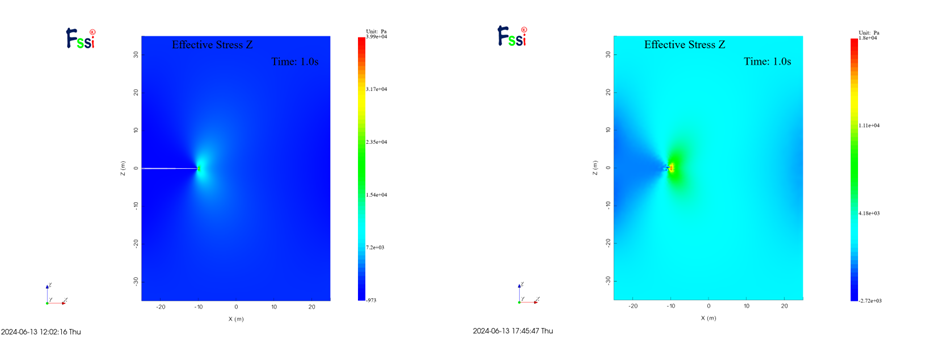
图 3-11 σyy计算结果云图对比
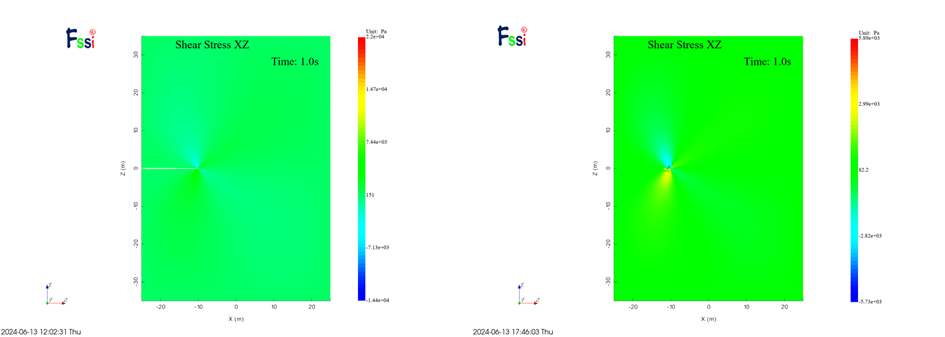
图 3-12 σxy计算结果云图对比
从云图结果看,两种建模方式对于位移的计算结果存在偏差,但应力计算结果基本相同,分析有可能是因为软件在处理共坐标节点过程中需要对重合节点进行特殊处理导致,但对于应力的影响较小。
提取θ = 0°测线上应力计算结果为例进行对比:
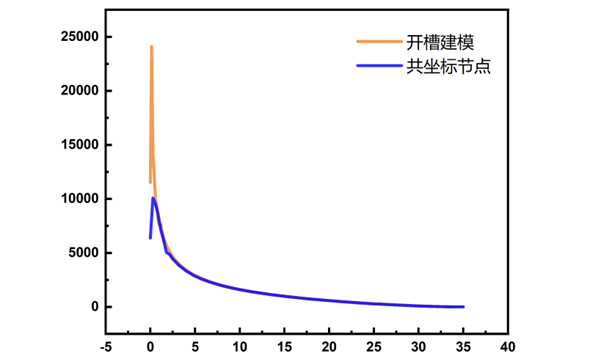
图 3-13 σxx计算结果
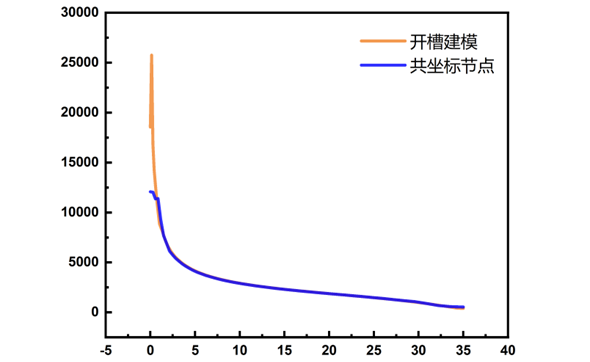
图 3-14 σyy计算结果
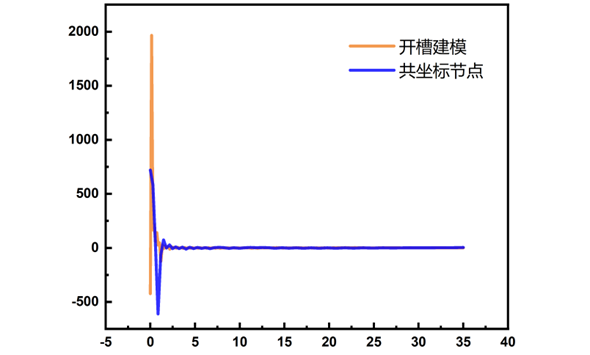
图 3-15 σxy计算结果
通过提取应力结果可以看出两种方案的计算结果基本上没有差异,但共坐标节点的处理方式在一定程度上降低了裂纹尖端奇异性对模拟结果的影响,使得裂纹尖端的应力结果波动相对于开槽建模而言较小。
同时共坐标节点的裂纹建模方式由于无需对尖端单元进行加密处理,大大降低了模型的单元数量,在本文的建模过程中,开槽建模方式单元数为12841个,而共坐标节点建模方式总单元数量仅为2651个。极大地提升了复杂模型下的计算速度,后续还需优化完善在位移计算过程中出现的问题。
3.3 本章小节
本章通过建立共坐标节点进行裂纹建模,证明了FssiCAS具备处理共坐标节点模型的能力,同时该建模方式对于缓解奇异点造成的应力梯度波动以及降低单元复杂程度具有较为明显的作用。
4 FssiCAS与FLAC3D计算结果对比
FssiCAS与FLAC3D分别代表两种计算方法,即有限单元法和有限差分法,通过对比两者的计算准确性与计算时间可以直观体现两种计算方法之间的差异。由于FLAC3D仅可计算三维模型,针对该对比测试进行单独三维建模。
考虑到两款软件均可读取Abaqus的网格文件,故建模过程仍在Abaqus中进行,与第二章中基本过程相同,仅仅加上模型的厚度,厚度设置为0.5m。最终建立三维模型如下:
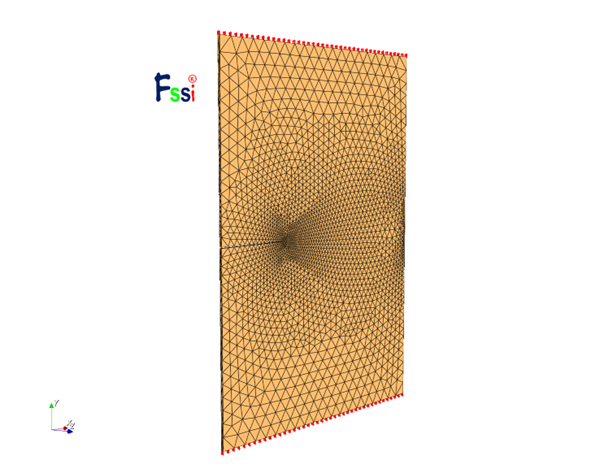
图 4-1 三维裂纹模型建立
在FssiCAS中设置边界条件与第二章中类似,但是将对于线设置改为对于单元面设置均布拉力,固定节点位置相同。附录二中为FLAC3D中的计算命令流,应力边界条件及位移边界条件和上述设置相同。
4.1 计算结果云图对比
提取两种方式下的计算云图进行对比,结果如下图所示。
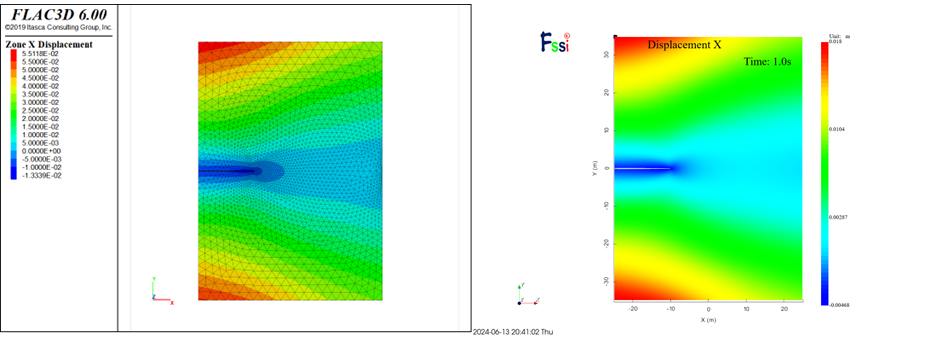
图 4-2 Ux计算结果云图对比
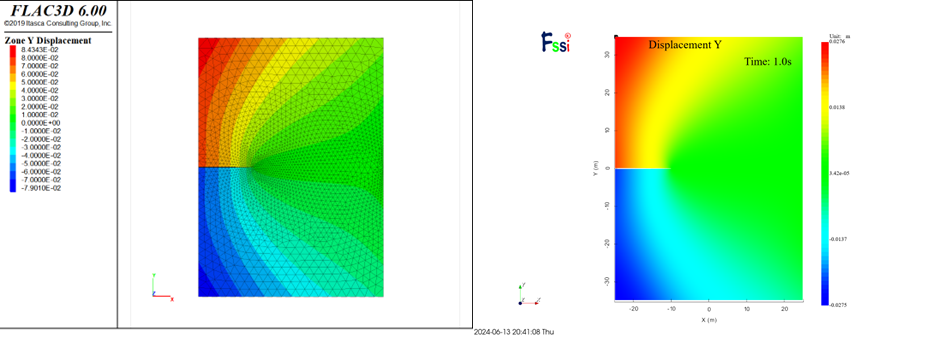
图 4-3 Uy计算结果云图对比

图 4-4 σxx计算结果云图对比
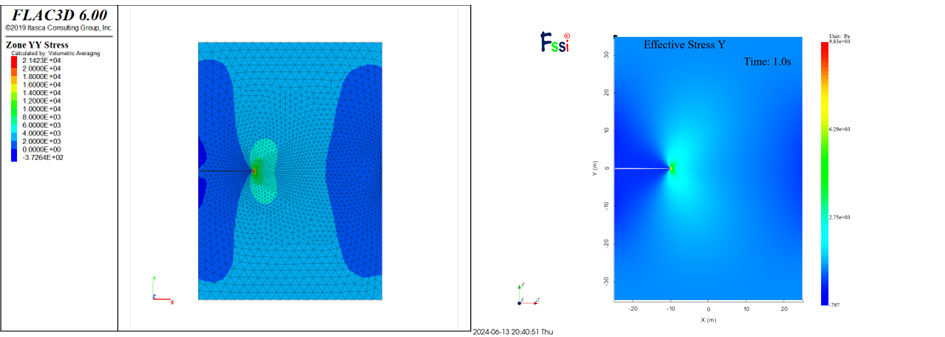
图 4-5 σyy计算结果云图对比

图 4-6 σxy计算结果云图对比
从应力云图以及位移云图的分布结果来看,两者计算差异较小,但应力峰值FLAC3D计算出的数值较大。
4.2 测线结果对比
进一步提取提取θ = 0°测线上应力计算结果进行对比:
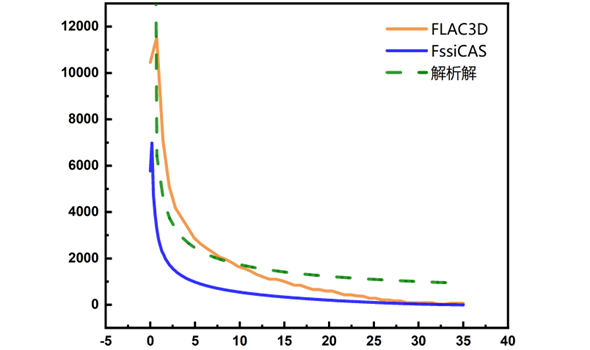
图 4-7 σxx计算结果
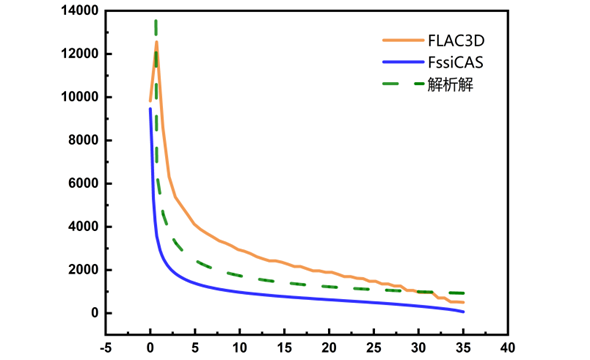
图 4-8 σyy计算结果
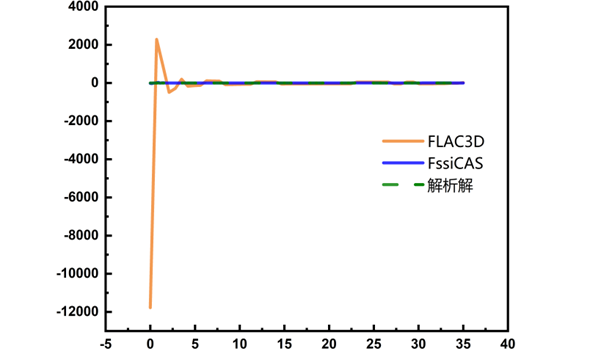
图 4-9 σxy计算结果
在三维上的计算结果,FssiCAS和FLAC3D显示出较大差异,对于σxx而言,FLAC3D在裂纹尖端解更接近解析解,但从整体应力分布形态而言,FssiCAS更为接近。而从σyy看,解析解处在两种计算方式之间,从形态上也更接近FssiCAS的计算结果。对于σxy的计算结果,FssiCAS更为准确,即便在奇异点附近也不存在应力的大范围波动,与解析解的拟合程度更高。
从计算时长对比,FLAC3D由于是有限差分法,其应力需要在单元节点之间进行迭代传递,由此导致计算时长较长,而FssiCAS为有限元计算,计算过程对于所有节点同时求解,因此求解时长较短,根据求解器日志,仅耗费2秒即可完成该三维模型的计算。
4.3 本章小节
本章对比了FssiCAS与FLAC3D在三维模型下的计算结果,两者的计算结果基本一致,在远端的边界效应相对于二维模型更为明显。但FssiCAS在处理裂纹尖端奇异点上优势明显,在奇异点波动较小。此外计算效率明显高于FLAC3D。
5 结论
本次通过对裂纹尖端的应力场位移场进行求解,全面对比了FssiCAS,Abaqus以及FLAC3D的计算差异,FssiCAS在计算效率上相较于其余两款软件有明显优势。在计算精度上,FssiCAS与Abaqus计算结果基本一致,通过与解析解的对比,说明可以较好地计算求解裂纹尖端应力场的应力分布情况。在三维模型的计算过程中,FssiCAS可以更好地处理裂纹尖端的奇异性问题,在奇异点处波动更小。
但本次模拟过程仍存在问题,首先是在模拟过程中发现若模型两侧网格划分不对称,在后续计算过程中有可能出现刚体旋转的结果,需要后续继续检查问题,同时在共坐标节点建模的尝试过程中,虽然一定程度上解决了裂纹尖端应力波动的问题,但对于位移场的计算仍存在一定问题需要解决。
FssiCAS可以较好的模拟裂纹尖端应力场及位移场,说明其可以处理由于奇异点导致的应力集中问题,具有良好的计算稳定性和准确性。
参考文献
[1] 程靳, 赵树山. 断裂力学[M]. 科学出版社, 2006.